Funciones
Noción de Función
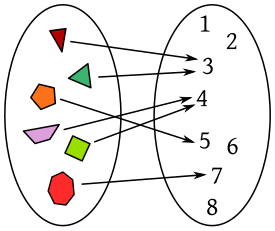
Función
Dados dos conjuntos A y B, una función F de A a B denotado como F: A - B asignada Acada elemento de A exactamente un elemento de B.
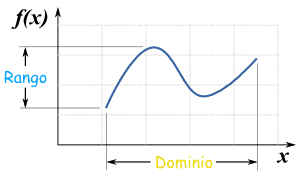
Dominio, Codomino, Rango
En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan.
Pero de hecho son conceptos importantes cuando se define una función. ¡Sigue leyendo!
Función es aquella relación en la que a cada elemento del dominio le corresponde un solo elemento del contradominio.
Función
Dados dos conjuntos A y B, una función F de A a B denotado como F: A - B asignada Acada elemento de A exactamente un elemento de B.
Dominio, Codomino, Rango
En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan.
Pero de hecho son conceptos importantes cuando se define una función. ¡Sigue leyendo!
Tipos de Funciones
Función inyectiva
Es inyectiva si a elementos distintos del conjunto  les corresponden elementos distintos en el conjunto
les corresponden elementos distintos en el conjunto  de
de  .
Es decir, cada elemento del conjunto Y tiene a lo sumo una antiimagen
en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más
elementos que tengan la misma imagen.
.
Es decir, cada elemento del conjunto Y tiene a lo sumo una antiimagen
en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más
elementos que tengan la misma imagen.
 les corresponden elementos distintos en el conjunto
les corresponden elementos distintos en el conjunto  de
de  .
Es decir, cada elemento del conjunto Y tiene a lo sumo una antiimagen
en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más
elementos que tengan la misma imagen.
.
Es decir, cada elemento del conjunto Y tiene a lo sumo una antiimagen
en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más
elementos que tengan la misma imagen.
Frunción Sobreyectiva
Es sobreyectiva (epiyectiva, suprayectiva, suryectiva, exhaustiva o subyectiva), si está aplicada sobre todo el codominio, es decir, cuando cada elemento de "Y" es la imagen de como mínimo un elemento de "X".
Función Biyectiva
Es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada y a cada elemento del conjunto de llegada le corresponde un elemento de conjunto de salida.




No hay comentarios:
Publicar un comentario